Кристаллографическая символика

Ученые выработали специальные приемы, позволяющие обозначить положение граней в координатной системе, а тем самым и друг относительно друга. С этими обозначениями полезно познакомиться, чтобы лучше понимать язык кристаллографов и минералогов.

Условимся не делать различия между параллельными гранями. Такие грани входят в один пакет плоских сеток, одинаково ориентированы в структуре, физически идентичны. Поскольку нас интересует только угловая ориентировка грани, мы можем ее зафиксировать отношением отрезков, которые грань отсекает на координатных осях. Из рис. 9, а видно, что это отношение в силу подобия фигур остается постоянным для всех параллельных граней данного направления. Упростим задачу: 1) перенесем нашу грань параллельно первоначальному положению так, чтобы она пересекала координатные оси в узлах пространственной решетки; 2) выразим отсекаемые осевые отрезки в числах m, n, р параметров элементарной ячейки - эти числа всегда целые. Пусть, например, плоскость грани отсекает на оси I четыре параметра во, на оси II - четыре параметра b_o и на оси III - шесть параметров с_о. Получаем для данной грани m:n:p= = 4:4:6 = 2:2:3.

Но когда грань параллельна одной из координатных осей, отрезок надо считать "бесконечным", что неудобно. Поэтому вместо отношения отрезков условились пользоваться отношением обратных им величин 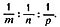. Это отношение приводят к целым числам, а знаки деления опускают.

Например, 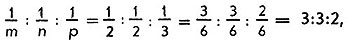символ данной грани (332). Все три числа - индексы - читаются отдельно: "три, три, два". При такой, системе обозначений индекс грани, параллельной координатной оси, равен нулю: (120) - грань параллельна оси III, (001) - осям I и II, (101) - оси II. Если грань пересекает координатную ось в ее отрицательной части, соответствующий индекс отрицателен: (001) - "ноль, ноль, минус один". Когда символы двух граней отличаются только одним индексом, больший угол с соответствующей координатной осью составляет грань с большим индексом. Так, грань (201) пересекает ось I под большим углом, чем грань (101) в той же координатной системе.

Указывая угловую ориентировку грани относительно осевого креста, символ грани выполняет и другую важную функцию: определяет положение грани в пространственной решетке, в структуре кристалла.

Существуют правила определения символов любых граней кристаллов. Читатель может познакомиться с ними по любому курсу кристаллографии.

В качестве символа простой формы служит символ одной из ее граней - ближайшей к наблюдателю. Чтобы не возникли путаницы, установка кристалла и координатная система должны быть выбраны правильно. Символ простой формы заключают в фигурные скобки. Так, в кубической сингонии символ {100} соответствует кубу с шестью гранями (100), (010), (001), (100), (010) и (001), первая из них "представляет" форму в целом (рис. 9, б). Необходимо обратить внимание: в разных сингониях один и тот же символ может соответствовать разным простым формам. Тем же символом {100} в тетрагональной сингонии обозначена тетрагональная призма с четырьмя гранями (100), (010), (100) и (010) (рис. 9, д), а в ромбической, моноклинной и триклинной сингониях - ромбическая призма, пинакоид и моноэдр. В григональнсй и гексагональной сингониях, где применяется четырехосная система координат, символы граней и простых форм состоят из четырех индексов: (1010), {0001} и т. д.

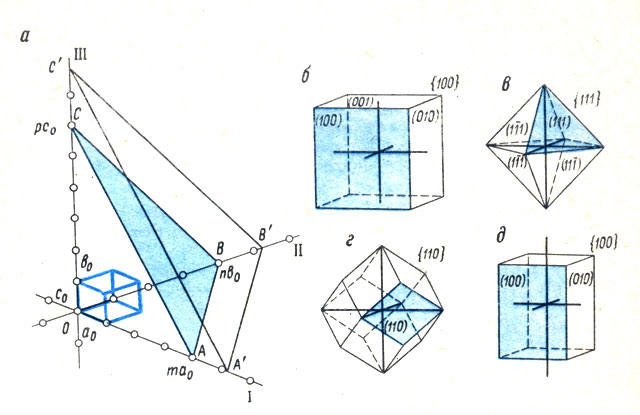
Рис. 9. Символика граней кристаллов. Грань А'В'С' можно параллельным переносом привести в положение ABC, когда она пересекает координатные оси в узлах решетки (а). Кристаллографические символы граней куба (б), октаэдра (в), ромбододекаэдра (г), тетрагональной призмы (д)

Напомним, что масштабы измерения отрезков по разным осям в общем случае не совпадают: ведь за единицы измерения мы выбрали разные параметры элементарной ячейки. Поэтому равенство индексов само по себе не говорит о том, что грань одинаково расположена по отношению к соответствующим осям. Такой вывод был бы безусловно справедлив только в случае кристалла кубической сингонии, где элементарная ячейка всегда имеет равные ребра и прямые углы. На рис. 9, в, г, видно, что грани октаэдра {111} расположены под одинаковыми углами ко всем трем осям и отсекают от них равные отрезки, а грани ромбододекаэдра {110} таким же образом расположены к двум осям, будучи параллельны третьей. В тетрагональной сингонии аналогичное правило распространяется на первые два индекса, в тригональной и гексагональной - на первые три. В низших сингониях равным индексам соответствуют неравные осевые отрезки и неравные углы.

В триклинной сингонии возможны моноэдры и пинакоиды любых символов. В остальных сингониях возникают ограничения, налагаемые симметрией: в моноклинной сингонии хотя бы один индекс в символе моноэдра или пинакоида должен быть равен нулю, а в ромбической - два; в тетрагональной сингонии возможны пинакоиды и моноэдры только вида {001}, в тригональной и гексагональной - {0001}. В высшей категории эти формы невозможны. Читателю не составит большого труда убедиться в правильности этих положений.