Многообразие: проблема простого и сложного

Многообразие форм кристаллов, разумеется, не исчерпывается видами симметрии. Так, два кристалла, изображенные на рис. 7, имеют один и тот же набор элементов симметрии L₃3L₂4P, но тем не менее различны по форме.

Простые кристаллографические формы

Все боковые грани кристалла, изображенного на рис. 7, а, можно получить из одной исходной плоскости, параллельной оси L₃. Повернем эту ось на один, полный оборот - и вместо одной получим три симметричные плоскости. На их пересечениях возникнут ребра, ограничивающие боковые грани кристалла. Тем же способом можно получить грани верхней половины другого кристалла (рис. 7, б), но исходная плоскость должна быть расположена наклонно к оси L₃; чтобы получить три нижние грани, следует дополнительно воспользоваться горизонтальной плоскостью симметрии. В том и другом случаях построение привело к появлению новых элементов симметрии - трех L₂ и трех Р. С их помощью также можно было бы получить найденные грани, даже не пользуясь осью L₃.

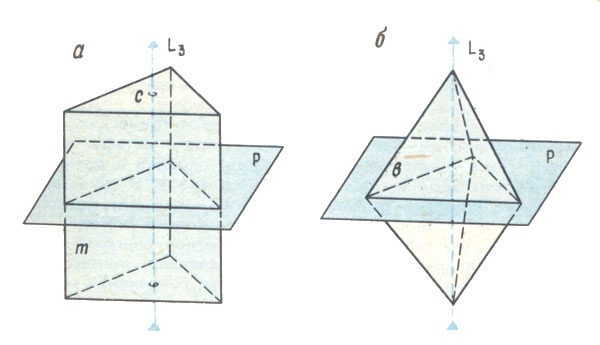
Рис. 7. Образование простых форм кристаллов

Совокупность граней, получаемых с помощью элементов симметрии из одной исходной плоскости, называется простой кристаллографической формой. В наших примерах элементы симметрии одинаковы, но исходные плоскости различны, а потому получились и различные простые формы. Все грани одной простой формы обозначим одной буквой, как это принято в кристаллографии.

С помощью оси и плоскости симметрии все огранение правого кристалла получается из единственной исходной плоскости. Для левого - исходных плоскостей требуется две: m - параллельная оси L₃ и с - перпендикулярная L₃ и параллельная Р. Огранение левого кристалла - комбинация двух простых форм m и с, причем форма с состоит всего из двух граней.

И вообще, любой кристалл огранен одной простой формой либо комбинацией простых форм. При отсутствии искажений все грани одной простой формы одинаковы - такие кристаллы называются правильно ограненными. Размеры и очертания граней простой формы зависят от комбинации с другими формами; преобладающая простая форма определяет габитус комбинации. Грани одной простой формы одинаковы по твердости, растворимости, электрическим, тепловым и другим физическим свойствам, деталям окраски, штриховке и другой "скульптуре", отражающей многосложную историю формирования кристалла. И наоборот, грани разных простых форм обычно отличаются рельефом поверхности и свойствами. В этом - одно из проявлений анизотропии кристаллов - неодинаковости свойств по разным направлениям.

Систематика простых форм

Из рис. 7 видно, что одной простой формы не всегда достаточно для огранения кристалла. Правый кристалл огранен единственной простой формой b. На левом же кристалле ни форма m, ни форма с не могли бы выполнить эту роль по ртдельности: многогранник остался бы незамкнутым. Форма b - закрытая простая форма, m и с - открытые. Закрытые формы участвуют в огранении кристаллов в комбинациях и поодиночке, открытые - только в комбинациях.

Названия простых форм образованы от греческих корней: моно - один, ди - два, три - три, тетра - четыре, пента - пять, гекса - шесть, окта - восемь, додека - двенадцать, гон - угол, эдра - грань, пинакс - доска и т. д. Распространенные простые формы кристаллов показаны на рис. 8.

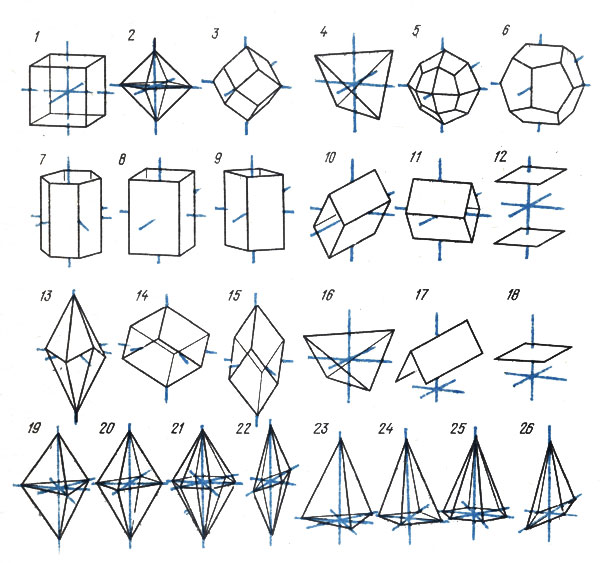
Рис. 8. Распространенные простые формы кристаллов: 1 - куб; 2 - октаэдр; 3 - ромбододекаэдр; 4 - тетраэдр; 5 - тетрагонтриоктаэдр; 6 - Пентагон додекаэдр; 7-11 - призмы: гексагональная (7), тетрагональная (8), ромбические (9-11); 12 - пинакоид; 13 - скаленоэдр; 14, 15 - ромбоэдры; 16 - ромбический тетраэдр; 17 - диэдр (дома); 18 - моноэдр; 19-22 - дипирамиды: тригональная (19), тетрагональная (20), гексагональная (21), ромбическая (22); 23-26 - пирамиды: тригональная (23), тетрагональная (24), гексагональная (25), ромбическая (26). В кубической сингонии встречаются формы 1-6; в тетрагональной - 8, 12, 18, 20, 24; в ромбической и моноклинной - 9-12, 16-18, 22, 26; в триклинной - 12, 18; в тригональной - 7, 12, 13-15, 18, 19, 21, 23, 25; в гексагональной - 7, 12, 18, 21, 25

Одни простые формы свойственны только определенным сингониям, другие - разным. В кубической сингонии, кроме куба и октаэдра, возможны ромбододекаэдр, пентагондодекаэдр (грани - неравносторонние пятиугольники), тетраэдр (форма молочного пакета) и др. Простые формы кубической сингонии имеют четное число граней (до 48), все они без исключения закрытые и в других сингониях не встречаются.

В средней категории, напротив, распространены открытые простые формы с малым числом граней - моноэдр (одна грань) и пинакоид (две параллельные грани). Этим граням "разрешено" занимать только одно положение - перпендикулярно главной оси, иначе их было бы соответственно больше, и тогда получились бы уже другие простые формы - призмы (грани параллельны главной оси) или пирамиды (грани наклонны к главной оси). Те и другие в зависимости от порядка главной оси бывают тетрагональными (поперечное сечение - квадрат), тригональными (равносторонний треугольник), гексагональными (равносторонний шестиугольник), а также с удвоенным числом граней. В отличие от геометрических призм и пирамид они имеют только боковые грани, будучи, таким образом, открытыми формами. При наличии плоскости симметрии, перпендикулярной главной оси, получаются дипирамиды - закрытые формы.

Кристалл, изображенный на рис. 7, б, огранен тригональной дипирамидой; на рис. 7, а - комбинацией тригональной призмы и пинакоида.

В низшей категории часто встречаются пинакоиды и моноэдры, ромбические призмы, пирамиды и дипирамиды (поперечное сечение - ромб). Специфические для этой категории формы - диэдр и ромбический тетраэдр.

Хаос и порядок

Сколько существует форм кристаллов? Много! Даже очень много! Увы, едва ли такая констатация заметно расширит наши представления о кристаллах. Попробуем поставить вопрос иначе: сколько существует простых форм? На это уже можно ответить конкретнее.

Будем рассуждать так: исходная плоскость параллельна, перпендикулярна или наклонна к тому или иному элементу симметрии; всего сочетаний элементов симметрии может быть 32; размножая плоскость симметрическими операциями, можно "синтезировать" любые простые формы. Делалось это не один раз и всегда с одним и тем же результатом: возможны простые формы кристаллов 47 типов. Получается, что не так уж и много?

Но ведь малочисленность типов совсем не означает малочисленности самих простых форм! Наклонное положение исходной плоскости - это на самом деле не одно, а множество различных положений. Например, ромбоэдры можно образовать при разных наклонах граней к оси L₃ (см. рис. 8, 14 и 15), получая "уплощенные", "острые" и даже "острейшие" ромбоэдры. Добавим сюда бесчисленные комбинации простых форм: многообразие форм кристаллов невозможно охватить мысленным взглядом.

Но, с другой стороны, просто бесконечное разнообразие было бы не чем иным, как хаосом, беспорядком. Такого хаотического, случайного многообразия мы не наблюдаем нигде в природе - везде своя система. Недаром лучшие умы науки о кристаллах так настойчиво искали общие закономерности их формы. И оказалось, что все бесконечное разнообразие кристаллов укладывается в 47 типов простых форм и 32 математически строгих закона симметрии!

Обозревая царство минералов в целом, можно увидеть следующую картину: кристаллы 12,5% минеральных видов принадлежат к высшей категории симметрии, 26,5% - к средней и 61 % - к низшей категории.

Налицо столь явное преобладание низкосимметричных кристаллов, что напрашивается вопрос о причине.

На нее указывает установленный Е. С. Федоровым и П. Гротом закон, согласно которому симметрия кристаллов в общем понижается С усложнением их химического состава. Это легко понять: чем сложнее состав, тем меньше возможности построения высокосимметричных структур, так как в дело идут разнокалиберные строительные единицы - атомы разных элементов. Отсюда и тенденция к понижению внешней симметрии кристаллов. Закон Федорова - Грота имеет статистический характер: он относится к большим группам веществ, но не применим к отдельным соединениям. Так, гранат и азурит - кристаллографические антиподы (кубическая и моноклинная сингонии), хотя одинаковы по сложности состава - оба содержат по четыре различных элемента. Но в целом и минералы, и искусственные кристаллические вещества подчиняются закону Федорова - Грота: алмаз, большое число самородных металлов, сульфидов и оксидов (один или два элемента) относятся к кубической сингонии, в то время как минералы более сложного состава - силикаты, сульфаты и др. - занимают в основном нижние ступени иерархической лестницы симметрии.

С другой стороны, с усложнением состава численность минеральных видов растет, так как большее число элементов может образовать больше соединений. Этим и объясняется преобладание в царстве минералов представителей низшей категории симметрии. Оно станет еще заметнее, когда мы перейдем к рассмотрению кристаллов, несущих на себе следы влияния окружающей их среды.

А как обстоит дело с разнообразием кристаллических форм, если присмотреться к отдельным минеральным видам? По-разному. Галит, например, почти всегда встречается в виде кубов, хотя его класс симметрии допускает некоторые другие формы. Совсем иначе выглядит кальцит: на его кристаллах отмечено около 700 простых форм. Чтобы познакомиться со всеми формами минерала, требуется просмотреть множество образцов: на одном единственном кристалле полного набора простых форм не встретишь. Чертежи таких воображаемых "обобщенных" кристаллов можно увидеть только в справочниках, где им отдается предпочтение ради экономии места.

Эти любопытные факты, несомненно, должны привлечь наше внимание. Возьмем их на заметку, чтобы вернуться к ним, как и к другим "частностям", несколько позже.