Иерархия симметричности

Мы уже немного продвинулись в классификации кристаллов: распределили их по видам, или классам, симметрии.

Но при всем том более естественным кажется классифицировать кристаллы непосредственно по их форме. Ведь наш глаз, можно сказать, самой природой устроен так, чтобы быстро и безошибочно, без учебников и правил, замечать главные различия в форме предметов. Всякий с первого же взгляда отличит друг от друга детский кубик, карандаш, гайку, линейку, спичечный коробок. Хотя такие различия мы делаем автоматически, интуитивно, ничто не мешает нам проанализировать их. У кубика длина, ширина и высота Одинаковы, иначе говоря, облик его изометрический. Карандаш имеет облик удлиненный, столбчатый, а гайка - таблитчатый; притом у обоих Предметов один размер значительно отличается от двух других, примерно одинаковых. Облик коробка, как и линейки, правильно назвать уплощенным: все три измерения различны.

А как все-таки отличаются эти предметы по симметрии? Немного подумав, вы согласитесь со следующим утверждением: предмет, у которого высота, длина и ширина различны, не может иметь осей симметрии порядка выше 2-го. Это следует отнести к нашему коробку и линейке. Облик шестигранного карандаша, как и гайки, в сильной степени определяется наличием единственной оси L₆. Что касается кубика, то в нем есть даже несколько осей высшего (выше 2-го) порядка - об этом мы уже говорили.

Тот факт, что облик предмета связан с его симметрией, для нас уже не новость. Но теперь мы попробуем использовать симметрию для классификации обликов - задачи, если вдуматься, совсем не простой.

Категории симметрии

До сих пор нам приходилось ограничиваться качественной оценкой симметрии. Последние примеры подсказывают, как можно различать предметы по степени симметричности. Видимо, кубик, как "симметричный со всех сторон", надо считать наиболее симметричным, симметрию гайки и карандаша следует признать средней, а линейки и коробка - самой низкой. Нетрудно видеть, что различия сводятся к числу осей высшего порядка. Учитывая их важную роль, мы будем называть эти оси главными. Возникает следующая иерархия симметричности идеальных кристаллических многогранников.

1. Высшая категория: главных осей несколько, как в кубе. Сюда попадут галит и магнетит (см. рис. 3, а, б). Кристаллы высшей категории изометричны и обязательно имеют по четыре оси L₃.
2. Средняя категория: главная ось только одна, как у карандаша и гайки. Сюда отнесем кристаллы с единственной осью высшего порядка: кварц (см. рис. 3, в), берилл, диоптаз, апофиллит (см. рис. 5). Для них характерны столбчатые и таблитчатые облики.
3. Низшая категория: главных осей нет совсем, как у коробка и линейки. Сюда попадут кристаллы уплощенного и асимметричного обликов: гемиморфит, аксинит, гипс, арагонит (см. рис. 3 и 5).

Читатель может почувствовать недоверие к нашим манипуляциям с симметрией: раз уж мы договорились о типах обликов, то почему бы не классифицировать кристаллы этим простейшим способом - на столбчатые, таблитчатые и т. д.?

В свое время кристаллография прошла через это. Однако, накопив достаточно сведений р кристаллах, ученые пришли к выводу, что облик - ненадежный признак. Среди кристаллов берилла, например, встречаются и "гайки", и "карандаши", но ведь минерал один и тот же. С точки зрения симметрии между "карандашом" и "гайкой" разницы нет. Выходит, симметрия - свойство и характерное, и устойчивое. Поэтому в основу классификации кристаллов была положена все-таки симметрия, а облик сохранил значение второстепенного признака. Этот выбор, явившийся результатом длительных поисков, сделал честь интуиции ученых, ибо, как выяснилось гораздо позже, симметрия тесно связана с главным в кристаллах - правильностью их внутреннего строения.

Кристаллографические сингонии

Пойдем дальше в нашей классификации кристаллов. Введем еще один признак: наличие или отсутствие перекосов. До сих пор мы принимали во внимание только соотношение длины, ширины и высоты, а теперь будем учитывать еще и важнейшие углы кристалла - так называемые габитусные углы. Взглянем с этой точки зрения еще раз на уже знакомые нам кристаллы. Кристалл аксинита (см. рис. 3, д) перекошен со всех сторон, а кристалл гипса (см. рис. 5, а) - только в "профиль". Кристаллы гемиморфита и арагонита (см., рис. 3, г и 5, б) совсем не имеют перекосов: габитусные углы попарно симметричны, и нетрудно заметить, что это связано с наличием достаточного числа осей 2-го порядка и плоскостей симметрии. По прочим признакам все названные кристаллы относятся к низшей категории. В средней категории все кристаллы без перекосов, но габитусные углы зависят от порядка главной оси: 3-го, как у диоптаза, 4-го, как у апофиллита, или 6-го, как у берилла (см. рис. 5). В высшей категории габитусные углы симметричны со всех сторон.

После этой подготовительной работы мы сможем подразделить все кристаллические многогранники на семь систем, или кристаллографических сингонии (от греческого слова, означающего "сходноугольность").

В высшей категории окажется одна сингония, называемая кубической. Поскольку она единственная, ее признаки, очевидно, совпадут с признаками высшей категории кристаллов.

Средняя категория в зависимости от порядка главной оси разделится на три сингонии: гексагональную ("шестиугольную"), тригональную ("треугольную") и тетрагональную ("квадратную").

Низшая категория (главные оси отсутствуют) делится на ромбическую сингонию, в которой кристаллы не имеют "перекосов", моноклинную - с перекосом только в одной проекции (в профиль) и триклинную, где кристаллы перекошены, асимметричны со всех сторон.

Кристаллографические системы координат

Но кристаллография не была бы точной наукой, если бы ограничивалась наглядными представлениями. Она широко пользуется строгими математическими методами и приемами, один из которых - введение кристаллографических систем координат.

За начало координат примем геометрический центр идеализированного кристалла, а оси направим вдоль важнейших ребер или по главным осям симметрии. Такая система координат отличается от широко известной прямоугольной системы тем, что углы между осями - не обязательно прямые, а зависят от габитусных углов каждого конкретного кристалла.

Условимся всегда располагать кристалл так чтобы главная ось проходила вертикально. Если её нет, повернем кристалл так, чтобы вертикальной оказалась группа наиболее выраженных параллельных ребер. Тогда одна из координатных осей тоже займет вертикальное положение; присвоим ей обозначение III. Две другие оси выберем так: одну направим к себе и назовем осью I; другую направим вправо, и пусть это будет ось II. (На всех предыдущих рисунках кристаллы изображены именно в такой "кристаллографической установке"). Координатную систему будем характеризовать отрезками осей а, b, с от центра до пересечения с гранями и углами α, β, γ между осями. Получается "осевой крест" - что-то вроде скелета кристалла, выражающего общий характер его симметрии и внешнего облика. При классификации кристаллов осевой крест избавит нас от необходимости входить в подробности формы каждого экземпляра со всеми его гранями, ребрами и вершинами.

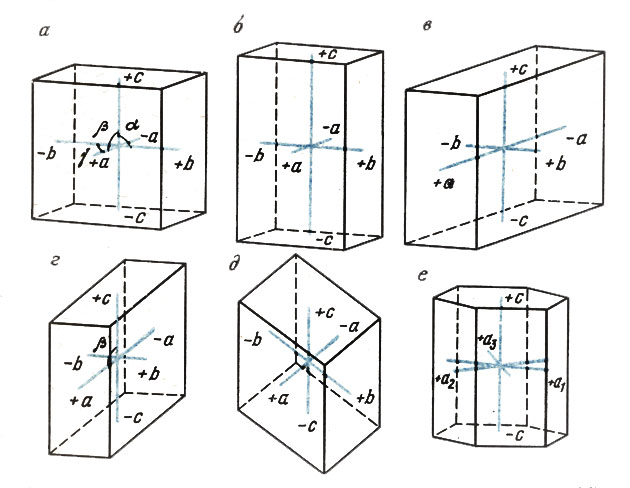
Рис. 6. Осевые кресты в кубической (a), тетрагональной (б), ромбической (в), моноклинной (г), триклинной (д), тригональной и гексагональной (е) сингониях

Наша следующая задача - выявить возможные типы осевых крестов, изменяя оси и углы.

Тип 1 - все оси равны, все углы прямые: а=b=с, α=β=γ=90° (рис. 6, а). Кристаллы с такими осевыми крестами могут быть только в кубической сингонии.

Тип 2 - углы прямые, но равны только две оси: а-b≠с, α=β=γ= 90° (рис. 6, б) - тетрагональная сингония.

Тип 3 - все оси различны, углы прямые: ромбическая сингония (рис. 6, в).

Тип 4 - оси различны, одий из углов непрямой: а≠b≠c, α=γ=90°, β>90° (рис. 6, г). "Перекос" в одном направлении говорит о Принадлежности к моноклинной сингонии.

Тип 5 - оси различны, все углы непрямые: а≠b≠с, α>90°, β>90°, γ>90° - триклинная сингония (рис. 6, д).

Тип 6. Для кристаллов с единственной главной осью L₃ или L₆ удобнее четырехосная система координат (рис. 6, е), в которой три равные оси лежат в горизонтальной плоскости под углами 120° друг к другу, а четвертая перпендикулярна им и совпадает с главной осью кристалла. Такая система координат хорошо подойдет для кристаллов тригональной и гексагональной сингонии^*.

^* (В некоторых руководствах обе эти сингонии объединяются в одну, называемую гексагональной.)

Этим возможные варианты исчерпываются. Первые пять типов осевых крестов однозначно соответствуют пяти сингониям, а шестой тип - одновременно двум сингониям: тригональной и гексагональной.

Подведем итог. Иерархия симметричности кристаллов выглядит следующим образом. По наличию главных осей (т. е. осей симметрии порядка выше 2-го) все кристаллы делятся на три категории, объединяющие семь сингонии, в каждую из которых входят кристаллы с однотипными осевыми крестами. В свою очередь сингонии по сочетаниям элементов симметрии делятся в общей сложности на 32 класса. Как видим, критерий симметрии весьма эффективен: он обеспечивает каждому минералу при всем разнообразии его формы свое место в систематике кристаллов.

Методы работы профессионалов

Если минерал известен, то мудрить с определением его сингонии нет надобности - достаточно раскрыть на нужной странице справочник. А вот когда минерал неизвестен и о сингонии можно судить только по самому кристаллу, специалисту приходится потрудиться - ведь его устраивает лишь достоверный ответ. Вплоть до 20-х годов нашего века единственным средством для этого было измерение кристаллов на специальных приборах - гониометрах. С течением времени гониометры совершенствовались и достигли высокой точности. Но если нет индивидов с собственной кристаллической огранкой, гониометрический метод бессилен. Увы, хорошо ограненные природные кристаллы в основном уже изучены, и ныне ученые, открывая новые минеральные виды, чаще всего вынуждены иметь дело с мелкими бесформенными зернышками. Минералогическая систематика давно топталась бы на месте, если бы ее развитие зависело от совершенства добытых кристаллов новых минералов.

Выход был найден в принципиально ином подходе к задаче - на основе связи внешней симметрии кристаллов с их внутренним строением. Правда, как определять характеристики структур, стало ясно лишь в первой четверти нашего века. Зато в ближайшие десятилетия в изучении структур было достигнуто несравненно больше, чем за всю предшествующую историю науки. Идея соответствия внешней формы и структуры кристалла - ключевая в современной кристаллографии.

Обратимся вновь к пространственной решетке кристалла (см. рис. 1). Наименьший из повторяющихся "кирпичей" называется элементарной ячейкой (см. рис. 1, г). Она может иметь форму либо параллелепипеда (в частном случае куба или квадратной призмы), либо шестигранной призмы, и в одной и той же ориентировке, без поворотов и без пропусков, повторяется во всем объеме кристалла, сплошь заполняя пространство. На рис. 1, б элементарная ячейка выделена в нижнем углу решетки. Чтобы описать всю геометрию элементарной ячейки, достаточно всего шести величин: длин трех ее ребер - параметров ао, bо, cо и углов α, β, γ между ребрами. Симметричную ячейку описать еще проще: для кубической, например, достаточно всего одной величины - параметра ао: ведь остальные параметры такие же, а все углы - прямые.

Сопоставив рис. 1, б и г, можно видеть, что элементарная ячейка дает полное представление о структуре кристалла. С другой стороны, ячейка связана с его внешней формой. Важнейшие ребра кристалла - это ряды пространственной решетки. Следовательно, координатные оси должны располагаться вдоль ребер элементарной ячейки. Ячейка как бы содержит осевой крест "в миниатюре": углы те же, отношение параметров а_о, b_о, c_о равно отношению координатных осей а, b, с. В самом деле, многогранники, в которые вписаны осевые кресты (см. рис. 6), вполне могли бы по своей форме претендовать на роль элементарных ячеек в соответствующих сингониях. Так, в кубической сингонии элементарная ячейка имеет форму куба, в тетрагональной - правильной четырехгранной призмы, в гексагональной - правильной шестигранной призмы и т. д.

Итак, элементарная ячейка заключает признаки сингонии. Сингонией можно назвать совокупность видов симметрии кристаллов со сходными характеристиками элементарных ячеек.

Это определение отвечает поставленной цели: связывает внешнюю симметрию с внутренним строением кристалла. Дело за тем, чтобы распознать элементарную ячейку. Но как это сделать? Конечно, не может быть и речи о том, чтобы разглядеть ее в микроскоп, пусть даже самый сильный: параметры элементарных ячеек имеют тот же порядок, что и размеры атомов - стомиллионные доли сантиметра. Все рассуждения о структурах оставались, строго говоря, в рамках гипотез, пока не появилась возможность проверить их опытным путем. Произошло это в начале нашего века благодаря открытию дифракции рентгеновских лучей при прохождении их через кристаллические тела. Это открытие лежит в основе современных методов рентгеноструктурного анализа, чрезвычайно широко применяемого в исследованиях кристаллов. Они позволяют быстро и точно находить характеристики кристаллических структур, представленных индивидами или обломками любой формы и размера, вплоть до порошка.

С тех пор кристаллографы, занимающиеся структурами, навсегда избавились от кабальной зависимости от качества кристаллов. Но в повседневной практике, когда приходится иметь дело с более или менее правильными кристаллами, определение сингонии на глаз сохраняет роль важного профессионального навыка, необходимого минералогу так же, как инженеру - навык различать по внешнему виду сортаменты стального проката, болтов, гаек.

Учение о сингониях ("системах") разработано немецким кристаллографом X. Вейсом (1780-1856) и австрийским минералогом Ф. Моосом (1773-1839) - прославленным автором шкалы твердости минералов. Основные положения этого учения сохранили свое значение до сих пор. Научный подвиг, X. Вейса и Ф. Мооса мог быть оценен по достоинству лишь при нынешнем уровне знаний о природе кристаллов. А ведь в то время само представление о симметрии кристаллов только зрело в сознании ученых!

Первый гониометр, изобретенный помощником Ромэ-Делиля французом М. Каранжо в 1782 г., представлял собой комбинацию транспортира и линейки, которые для измерения гранных углов прикладывали к кристаллу. Позже на смену прикладному гониометру пришел отражательный (У. X. Волластон, 1809 г.); для измерения углов в нем использовалось отражение гранями пучка света. Отражательный гониометр был коренным образом усовершенствован одновременно и независимо друг от друга выдающимися кристаллографами Е. С. Федоровым (1853-1919) и В. Гольдшмидтом (1853-1933).

В 1855 г. О. Браве сделал вывод всех типов пространственных решеток и элементарных ячеек. В 1890 г. Е. С. Федоров дал исчерпывающий анализ симметрии кристаллических структур. Основы кристаллохимии - современного учения о структурах кристаллов - заложены в начале нашего века Е. С. Федоровым и немецким минералогом П. Гротом (1843-1927).

Открытие дифракции рентгеновских лучей в кристаллах (1912 г.) принадлежит немецкому физику М. Лауэ (1879-1960); им же был разработан один из методов рентгеноструктурного анализа. Крупнейшие вклады в создание этих методов внесли Г. В. Вульф (Россия, 1913 г), У. Г. и У. Л. Брэгги - отец и сын (Англия, 1913 г.), П. Дебай и П. Шеррер (Германия, 1916 г.). Рентгеноструктурный анализ вскоре получил широкое признание, и гониометрический метод постепенно утратил свое значение в определении сингоний, но продолжает использоваться для изучения формы кристаллов.