"Кристаллы блещут симметрией"

В обыденной жизни мы привыкли просто любоваться кристаллами и редко задумываемся, почему они красивы. Теперь, когда мы намерены раздвинуть горизонты мира удивительного и прекрасного, приобщившись к науке о кристаллах, придется осваиваться с новыми понятиями, а главное - приучить себя смотреть на кристаллы глазами аналитика: сравнивать, классифицировать, выделять основное. И в этом тоже можно найти немалое удовольствие.

Видный советский ученый И. И. Шафрановский пишет: "В ограненном кристалле само природное явление как бы ставит готовую, хорошо сформулированную задачу, решение которой невозможно без углубленных геометрических изысканий". Чтобы лучше обозначить эту задачу, поступим так, как поступил бы на нашем месте исследователь: сузим круг вопросов. Займемся общим, временно пожертвовав частным. Для этого надо будет ограничиться идеальными экземплярами кристаллов: типичные, общие черты на них заметнее. Искаженные кристаллы вроде изображенных на рис. 2, кривые ребра, неровные грани - на все это есть свои причины, безусловно заслуживающие нашего внимания. Но всему свое время. Итак, будем говорить о главном - об идеальных или идеализированных кристаллах.

Как очень характерное свойство обращает на себя внимание правильное чередование, повторение одинаковых граней, ребер, вершин - симметрия кристаллических многогранников. Именно симметричностью так ласкают взор кристаллы. Это без лишних слов выражено принадлежащим знаменитому кристаллографу Е. С. Федорову афоризмом, вынесенным в заголовок. Симметричны грани, вершины и ребра кубика галита (рис. 3, а), и какой бы стороной мы ни положили его на стол, разницы не заметим. Про этот кристалл, равно как и про октаэдр магнетита (рис. 3, б), нельзя сказать: расположен вертикально, расположен горизонтально. Эти положения просто неразличимы. Невозможно указать, где у таких кристаллов верх, низ, длина, ширина, высота.

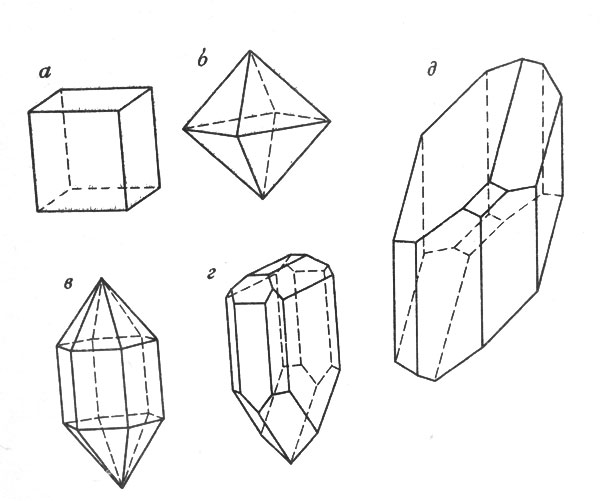
Рис. 3. Кристаллы различных минералов различны по симметрии: а - галит; б - магнетит; в - горный хрусталь; г - гемиморфит; д - аксинит

Иначе обстоит дело с кристаллом горного хрусталя (рис. 3, в). Неотличимы друг от друга те несколько положений, когда кристалл лежит на столе одной из боковых граней; нет разницы и между положениями вверх одним или другим концом. Но горизонтальное положение можно безошибочно отличить от вертикального - длина и ширина кристалла определенно различны.

Кристалл гемиморфита (рис. 3, г) имеет и длину, и ширину, и высоту. Ему можно придать не только два разных вертикальных положения, но и два разных горизонтальных: плашмя (двумя способами) и "на ребро" (тоже двумя способами).

Еще менее симметричен кристалл аксинита (рис. 3, д ): ему можно придать множество различных, неповторяющихся положений.

Итак, симметрия симметрии рознь. Симметричны все кристаллы, но по-разному.

Слагаемые симметрии

Чтобы как следует во всем этом разобраться, "расчленим" симметрию на отдельные составляющие. Для этого прибегнем к специальным геометрическим образам - элементам симметрии. В кристаллах наиболее важны центры, оси, плоскости симметрии. Не следует думать, что они физически существуют в кристаллах: эти точки, прямые и плоскости мы воображаем специально для того, чтобы описывать свойства симметричности, которыми обладает тот или иной кристалл.

Центр симметрии - точка внутри кристалла, делящая пополам любую проведенную через нее прямую, ограниченную поверхностью кристалла. В "центросимметричном" кристалле все точки (в частности, вершины) - соответственные, парные, а все прямые, соединяющие парные точки, пересекаются в центре симметрии. Из парных точек складываются парные ребра и парные грани; в центросимметричном кристалле они всегда перевернуты друг относительно друга (но не обязательно должны отличаться друг от друга). На чертежах кристаллов центр симметрии отмечают точкой и обозначают буквой С.

Центр симметрии имеется в кубе, октаэдре и во многих других многогранниках гораздо менее симметричной формы (рис. 4, а). Из рис. 3, г заключаем, что в кристалле гемиморфита центра симметрии нет.

На первый взгляд, центр симметрии как будто есть в кристалле горного хрусталя (см. рис. 3, в). На самом деле это не так: внимательное изучение показывает, что головки кристалла огранены нецентросимметричными гранями.

Горный хрусталь (кварц) обладает ценнейшим свойством - способностью электризоваться при сжатии или растяжении. Такие тела называются пьезоэлектриками. Они широко используются в разнообразных технических устройствах - датчиках механических напряжений, стабилизаторах частоты и др. Некоторые кристаллы - пироэлектрики - электризуются при нагревании. Впервые это явление было обнаружено в опытах с кристаллами турмалина. Пьезо- и пироэлектриками могут быть только нецентросимметричные кристаллы.

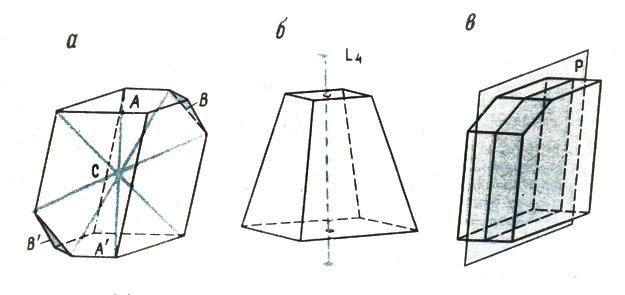
Рис. 4. Элементы симметрии кристаллов: центр (а); ось (б); плоскость (в)

Ось симметрии (рис. 4, б) - воображаемая прямая, при повороте вокруг которой кристалл дважды или более раз за один полный оборот совмещается со своим первоначальным положением. Количество этих совмещений называется порядком оси симметрии. Ось изображают прямой линией и обозначают буквой L с индексом, указывающим порядок. Осевая симметрия свойственна многим окружающим нас предметам. Карточные валеты, дамы и короли имеют оси симметрии 2-го порядка, перпендикулярные к плоскости карты. Кастрюля с двумя ручками тоже имеет ось симметрии L₂, а кастрюля без ручек - это "тело вращения" с осевой симметрией бесконечного порядка L_∞.

В кристалле может быть одна или несколько осей симметрии одинакового или разных порядков, а может не быть ни одной оси. В кубе, например, имеются: четыре оси L₃, каждая из которых проходит через две противолежащие вершины, совпадая с одной из пространственных диагоналей куба; три оси L₄, проходящие через центры противолежащих граней; шесть осей L₂, преходящих через середины противолежащих ребер. Все оси пересекаются в одной точке, которая в кубе служит центром симметрии.

В кристалле кварца продольная ось служит осью L₃; кроме того, имеются еще три оси L₂, каждая из которых проходит через середины противолежащих боковых ребер. Все эти четыре оси опять-таки пересекаются в одной точке.

Кристалл гемиморфита имеет только одну ось симметрии 2-го порядка. Ее легко найти, пользуясь рис. 3, г. В кристалле аксинита (см. рис. 3, д) совсем нет осей симметрии.

В отличие от других симметричных предметов кристаллические многогранники могут иметь оси симметрии только 2-, 3-, 4- и 6-го порядков. Как и все специфические свойства кристаллов, это связано с упорядоченностью их внутреннего строения. Поясним это на модели "кирпичной кладки" (см. рис. 1, б). "Кирпичи" должны быть одинаковыми по размерам и форме, укладываться одним и тем же способом и заполнять пространство сплошь, без промежутков. Нетрудно убедиться, что для этого годятся только параллелепипеды и шестигранные призмы. При попытке заполнить пространство, скажем, пяти- либо семигранными призмами неизбежно останутся пустоты, и для кристаллов такие "кирпичи" не подойдут. В связи с этим для внешней формы кристаллов невозможны оси симметрии L₅, L₇ и т. д.

В формах органической природы такие оси, наоборот, широко распространены. Так, симметрия L, присуща цветам шиповника, морским звездам, многим мелким организмам. Уместно привести по этому поводу любопытное суждение крупнейшего советского кристаллографа академика Н. В. Белова: "Кристаллографический запрет 5-ной оси определяется невозможностью согласования ее (равно как и осей порядка выше шести) с решеткой, с "решетчатым состоянием" кристаллического вещества. И поэтому можно думать, что 5-ная ось является у мелких организмов своеобразным инструментом борьбы за существование, страховкой против окаменения, против кристаллизации, первым шагом которой была бы "поимка" решеткой живого организма".

Плоскость симметрии - воображаемая плоскость, делящая кристалл на две зеркально-равные части - одна часть как бы является зеркальным отражением другой. Зеркально равны правая и левая руки. Сложите их ладонями: разделяющая ладони плоскость - это плоскость симметрии. На кристалле с плоскостью симметрии обязательно найдется хотя бы пара граней, связанных между собой как предмет и его зеркальное отражение (рис. 4, в). В кубе девять плоскостей симметрии, в кристалле гемиморфита - две (найдите их), в кристалле аксинита - ни одной. Плоскость симметрии обозначают буквой Р.

Симметричность кристаллов представляется вполне очевидной, однако представление о ней вошло в науку лишь сравнительно недавно. Первым подчеркнул серьезное значение симметрии великий французский кристаллограф Рене Жюст Гаюи (1743-1822); его творчество оказало большое влияние на дальнейшее развитие кристаллографии главным образом разработкой проблемы внутреннего строения кристаллов. Понятия оси, плоскости и центра симметрии были позже сформулированы соотечественником Гаюи О. Браве (1811-1863).

Из существования в кристаллах различных элементов симметрии непреложным образом вытекают и законы их взаимодействия друг с другом. Пусть, например, известно, что в кристалле имеются ось L₆ и ось L₂. Могут ли они располагаться как угодно? Нет, мы не сможем представить себе ничего иного, кроме взаимно перпендикулярного расположения этих осей. Если бы они были расположены иначе, то после поворота вокруг L₂ появилась бы еще одна L₆, а это уже противоречило бы условию задачи. С другой стороны, наличие оси L₆ обязывает к тому, чтобы в таком кристалле было по крайней мере три оси L₂. Все элементы симметрии так или иначе взаимодействуют друг с другом, вследствие чего некоторые их комбинации в кристаллах невозможны, а некоторые обязательны. Так, осей 3-го порядка может быть одна, четыре или ни одной; 4-го порядка - одна, три или ни одной; 6-го порядка - одна или ни одной; все оси симметрии пересекаются в одной точке. Подсчитано, что в кристаллах возможны 32 сочетания, или вида (класса) симметрии. Вид симметрии обозначается формулой, в которой перечисляются элементы симметрии и их число. Так, вид симметрии куба и октаэдра 3L₄4L₃6L₂9РС; кристалла гемиморфита - L₂2Р и т. д. Существуют также сокращенные обозначения видов симметрии.

Каждый минеральный вид кристаллизуется только в одном классе симметрии. Это налагает на форму кристаллов определенные ограничения. Так, минерал, кристаллизующийся в классе симметрии 3L₄4L₃6L₂9PC, можно встретить в виде кубов, октаэдров и некоторых других многогранников, но нельзя встретить, например, в виде трехгранных призм - это уже другой класс.

Математический вывод возможных видов симметрии кристаллов впервые сделал в 1830 г. немецкий профессор И. Ф. Гессель (1796-1872), однако он не был замечен современниками. В 1867 г. русский академик А. В. Гадолин (1828-1892) независимо от Гесселя доказал существование 32 классов симметрии кристаллов. В этих 32 классах размещены все без исключения искусственные кристаллические вещества и все минеральные виды и разновидности.

Разминка для пространственного воображения

Рассмотрим еще несколько примеров, чтобы закрепить наши познания и навыки в определении симметрии кристаллов. Кристалл аксинита (см. рис. 3, д), как уже отмечалось, принадлежит к наименее симметричным: в нем не обнаруживается никаких элементов симметрии, кроме центра С. В кристалле гипса (рис. 5, а) есть плоскость симметрии, перпендикулярно к ней расположена ось симметрии 2-го порядка, а точка пересечения оси с плоскостью является центром симметрии. Формула симметрии кристалла гипса - L₂PC. В кристалле арагонита (рис. 5, б) к этим элементам симметрии добавляются еще две оси 2-го порядка и две плоскости симметрии - получается вид 3L₂3РС. На примере арагонита стоит задержаться. Его особенность вот в чем: верхняя половина кристалла симметрична нижней, левая - правой, передняя - задней. Симметрия - одновременно и осевая (оси L₂), и зеркальная (плоскости симметрии). Таковы далеко не все кристаллы. Например, верхняя и нижняя половины кристалла гемиморфита не симметричны ( см. рис. 3, г). Это значит, что нет ни горизонтальных осей L₂, ни горизонтальной плоскости, ни центра симметрии. Остается L₂2P - это и есть класс симметрии гемиморфита.

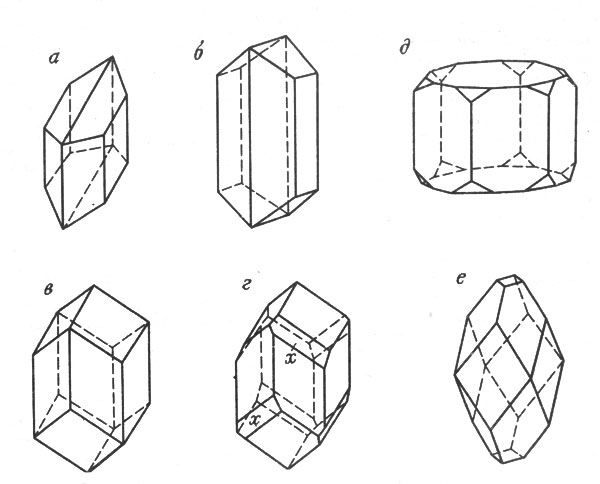
Рис. 5. Примеры кристаллов различных классов симметрии: а - гипс L₂PC; б - арагонит 3L₂3PC, в, г - диоптаз L₃С; д - берилл L₃6L₂7РС; е - апофиллит L₄4L₂5PC

В кристалле кварца (см. рис. 3, в) "верх" и "низ" симметричны, но в отличие от арагонита связаны только осями L₂ (их три), а плоскостей симметрии нет. Диоптаз (рис. 5, в) как будто имеет три вертикальные плоскости симметрии. Однако на некоторых кристаллах (рис. 5, г) есть небольшие грани х, присутствие которых нарушает зеркальную симметрию. Форма с большим числом граней является более общей. Почему на конкретных кристаллах возникают не все грани общей формы, мы выясним позже. А пока что мы обязаны учесть факт нарушения зеркальной симметрии: ведь те и другие кристаллы заведомо относятся к одному классу. Следовательно, диоптазу нужно приписать формулу симметрии L₃С вместо L₃3РС.

Ось симметрии L₆ легко обнаружить в кристалле берилла (рис. 5, д) класса L₆6L₂7РС. Оси L₂ расположены горизонтально: три проходят через середины противоположных ребер и еще три - через середины противоположных граней. Каждая ось L₂ лежит в одной из вертикальных плоскостей симметрии, и одновременно все они лежат в седьмой, горизонтальной плоскости симметрии.

Кристалл апофиллита (рис. 5, е) имеет вертикальную ось L₄, четыре вертикальные плоскости симметрии и одну горизонтальную, в которой лежат четыре оси L₂. На пересечении осей и плоскостей, как и в кристалле берилла, находится центр симметрии.

Подобные тренировочные "разминки" полезно повторять почаще. Выполняя упражнения самостоятельно, можно научиться быстро и почти машинально выявлять элементы симметрии кристаллов. А чертежи для упражнений можно найти в любом учебнике минералогии. Полезно потрудиться и над симметрией окружающих предметов: деревьев, животных, стола, книги, тарелки и др. Все предметы в той или иной мере симметричны, и особенно те, что сработаны руками человека. Подглядев когда-то симметрию у природы, человек убедился, что вещь симметричной формы удобна, а сделать ее намного проще. В сущности, придуманные человечеством машинные способы обработки материалов - точение, сверление, фрезерование, строгание, - сводятся к приданию вещам симметричной формы.